Jumat, Desember 11, 2015

MATRIKS MATEMATIKA

Dalam matematika, matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Contoh matriks dengan 2 baris dan 3 kolom yaitu
\begin{bmatrix}1 & 9 & -13 \\20 & 5 & -6 \end{bmatrix}.
Pemanfaatan matriks misalnya dalam menemukan solusi sistem persamaan linear. Penerapan lainnya adalah dalam transformasi linear, yaitu bentuk umum darifungsi linear, misalnya rotasi dalam 3 dimensi.
Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur.
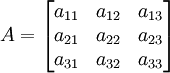
A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \!

Notasi[sunting | sunting sumber]

Matriks pada umumnya ditulis dalam tanda kurung siku/kurung kurawal:
\mathbf{A} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}.

Operasi dasar[sunting | sunting sumber]

Penjumlahan dan pengurangan matriks[sunting | sunting sumber]

Penjumlahan dan pengurangan matriks hanya dapat dilakukan apabila kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.
a_{ij} \pm b_{ij} = c_{ij}\!
atau dalam representasi dekoratfinya
\begin{bmatrix} {3} & {4} \\ {6} & {5} \\ \end{bmatrix} \!
\begin{bmatrix} (a_{11} \pm b_{11}) & (a_{12} \pm b_{12}) & (a_{13} \pm b_{13}) \\ (a_{21} \pm b_{21}) & (a_{22} \pm b_{22}) & (a_{23} \pm b_{23}) \\ \end{bmatrix} = \begin{bmatrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ \end{bmatrix} \!

Perkalian skalar[sunting | sunting sumber]

Matriks dapat dikalikan dengan sebuah skalar.
\lambda\cdot A := (\lambda\cdot a_{ij})_{i=1, \ldots , m; \ j=1, \ldots , n}
Contoh perhitungan :
5 \cdot \begin{pmatrix} 1 & -3 & 2 \\ 1 & 2 & 7 \end{pmatrix} = \begin{pmatrix} 5 \cdot 1 & 5 \cdot (-3) & 5 \cdot 2 \\ 5 \cdot 1 & 5 \cdot 2 & 5 \cdot 7 \end{pmatrix} = \begin{pmatrix} 5 & -15 & 10 \\ 5 & 10 & 35 \end{pmatrix}

Perkalian Matriks[sunting | sunting sumber]

Matriks dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom, lalu dijumlahkan pada baris yang sama.
c_{ij}=\sum_{k=1}^m a_{ik}\cdot b_{kj}
Contoh perhitungan :
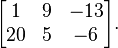
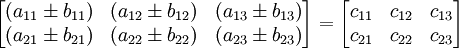
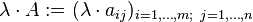
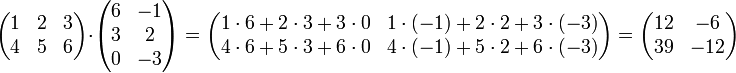
\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} \cdot \begin{pmatrix} 6 & -1 \\ 3 & 2 \\ 0 & -3 \end{pmatrix} = \begin{pmatrix} 1 \cdot 6 + 2 \cdot 3 + 3 \cdot 0 & 1 \cdot (-1) + 2 \cdot 2 + 3 \cdot (-3) \\ 4 \cdot 6 + 5 \cdot 3 + 6 \cdot 0 & 4 \cdot (-1) + 5 \cdot 2 + 6 \cdot (-3) \\ \end{pmatrix} = \begin{pmatrix} 12 & -6 \\ 39 & -12 \end{pmatrix}
Diposting oleh di

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)